Case Study Survival Design

Gernot Wassmer and Friedrich Pahlke

November 20, 2024

Case Study Survival Design

Survival Design

We wish to test

\(\hspace{2cm}H_0: \omega \geq 1 \text{ against } H_1: \omega < 1\)

We assume:

\(\alpha = 0.025\)
pi1 = 0.229, pi2 = 0.37 at 6 months
Power \(1 - \beta = 0.85\) at \(\omega = \frac{\ln(1 - \text{pi1})}{\ln(1 - \text{pi2})} = 0.563\)
Allocation ratio 1 : 1

`rpact` Planning

Start with fixed sample size (events) design:

library(rpact)
getSampleSizeSurvival(
  alpha = 0.025, 
  beta = 0.15, 
  hazardRatio = 0.563
) |> summary()

Sample size calculation for a survival endpoint

Fixed sample analysis, one-sided significance level 2.5%, power 85%. The results were calculated for a two-sample logrank test, H0: hazard ratio = 1, H1: hazard ratio = 0.563, control pi(2) = 0.2, event time = 12, accrual time = 12, accrual intensity = 57.4, follow-up time = 6.

Stage	Fixed
Stage level (one-sided)	0.0250
Efficacy boundary (z-value scale)	1.960
Efficacy boundary (t)	0.687
Number of subjects	689.1
Number of events	108.8
Analysis time	18.00
Expected study duration under H1	18.00

Legend:

(t): treatment effect scale

Required Number Of Events

109 events are needed to achieve 85% power for specified effect size

Required Number Of Subjects

Obviously, some default parameters were used to derive the required number of subjects

getSampleSizeSurvival(  
  alpha = 0.025, 
  beta = 0.15, 
  hazardRatio = 0.563) |> print()

Design plan parameters and output for survival data

Design parameters

Critical values: 1.960
Significance level: 0.0250
Type II error rate: 0.1500
Test: one-sided

User defined parameters

Hazard ratio: 0.563

Default parameters

Theta H0: 1
Type of computation: Schoenfeld
Assumed control rate: 0.200
Planned allocation ratio: 1
Event time: 12
Accrual time: 12.00
kappa: 1
Follow up time: 6.00
Drop-out rate (1): 0.000
Drop-out rate (2): 0.000
Drop-out time: 12.00

Sample size and output

Direction upper: FALSE
Assumed treatment rate: 0.118
median(1): 66.2
median(2): 37.3
lambda(1): 0.0105
lambda(2): 0.0186
Number of events: 108.8
Accrual intensity: 57.4
Number of events fixed: 108.8
Number of subjects fixed: 689.1
Number of subjects fixed (1): 344.6
Number of subjects fixed (2): 344.6
Analysis time: 18.00
Study duration: 18.00
Critical values (treatment effect scale): 0.687

Legend

(i): values of treatment arm i

Study specifications

accrual time = 24
study duration = 28
drop-out rate = 0.25 at 6 months
planned number of participants = 325

getSampleSizeSurvival(
    alpha = 0.025,
    beta = 0.15,
    pi1 = 0.229,
    pi2 = 0.37,
    eventTime = 6,
    accrualTime = 24,
    followUpTime = 4,
    dropoutRate1 = 0.25,
    dropoutRate2 = 0.25,
    dropoutTime = 6
) |> summary()

Study specifications

Sample size calculation for a survival endpoint

Fixed sample analysis, one-sided significance level 2.5%, power 85%. The results were calculated for a two-sample logrank test, H0: hazard ratio = 1, H1: treatment pi(1) = 0.229, control pi(2) = 0.37, event time = 6, accrual time = 24, accrual intensity = 10.8, follow-up time = 4, dropout rate(1) = 0.25, dropout rate(2) = 0.25, dropout time = 6.

Stage	Fixed
Stage level (one-sided)	0.0250
Efficacy boundary (z-value scale)	1.960
Efficacy boundary (t)	0.687
Number of subjects	259.2
Number of events	108.7
Analysis time	28.00
Expected study duration under H1	28.00

Legend:

(t): treatment effect scale

Follow-up time can be reduced with 325 participants:

getSampleSizeSurvival(
    alpha = 0.025,
    beta = 0.15,
    pi1 = 0.229,
    pi2 = 0.37,
    eventTime = 6,
    accrualTime = 24,
    maxNumberOfSubjects = 325,
    dropoutRate1 = 0.25,
    dropoutRate2 = 0.25,
    dropoutTime = 6
) |> summary()

Sample size calculation for a survival endpoint

Fixed sample analysis, one-sided significance level 2.5%, power 85%. The results were calculated for a two-sample logrank test, H0: hazard ratio = 1, H1: treatment pi(1) = 0.229, control pi(2) = 0.37, number of subjects = 325, event time = 6, accrual time = 24, accrual intensity = 13.5, dropout rate(1) = 0.25, dropout rate(2) = 0.25, dropout time = 6.

Stage	Fixed
Stage level (one-sided)	0.0250
Efficacy boundary (z-value scale)	1.960
Efficacy boundary (t)	0.687
Number of subjects	325.0
Number of events	108.7
Analysis time	23.18
Expected study duration under H1	23.18

Legend:

(t): treatment effect scale

Design with interim stage

designGS <- getDesignGroupSequential(
    directionUpper = FALSE,  
    alpha = 0.025,
    beta = 0.15,
    typeOfDesign = "asHSD",
    gammaA = -4.5,
    informationRates = c(50/77, 1)
) 
getSampleSizeSurvival(
    design = designGS,
    pi1 = 0.229,
    pi2 = 0.37,
    eventTime = 6,
    accrualTime = 24,
    followUpTime = 4,
    dropoutRate1 = 0.25,
    dropoutRate2 = 0.25,
    dropoutTime = 6
) |> summary()

Design with interim stage

Sample size calculation for a survival endpoint

Sequential analysis with a maximum of 2 looks (group sequential design), one-sided overall significance level 2.5%, power 85%. The results were calculated for a two-sample logrank test, H0: hazard ratio = 1, H1: treatment pi(1) = 0.229, control pi(2) = 0.37, event time = 6, accrual time = 24, accrual intensity = 10.9, follow-up time = 4, dropout rate(1) = 0.25, dropout rate(2) = 0.25, dropout time = 6.

Stage	1	2
Planned information rate	64.9%	100%
Cumulative alpha spent	0.0049	0.0250
Stage levels (one-sided)	0.0049	0.0235
Efficacy boundary (z-value scale)	2.580	1.985
Efficacy boundary (t)	0.543	0.685
Cumulative power	0.4388	0.8500
Number of subjects	219.7	261.7
Expected number of subjects under H1		243.3
Cumulative number of events	71.3	109.8
Expected number of events under H1		92.9
Analysis time	20.15	28.00
Expected study duration under H1		24.56
Exit probability for efficacy (under H0)	0.0049
Exit probability for efficacy (under H1)	0.4388

Legend:

(t): treatment effect scale

Results

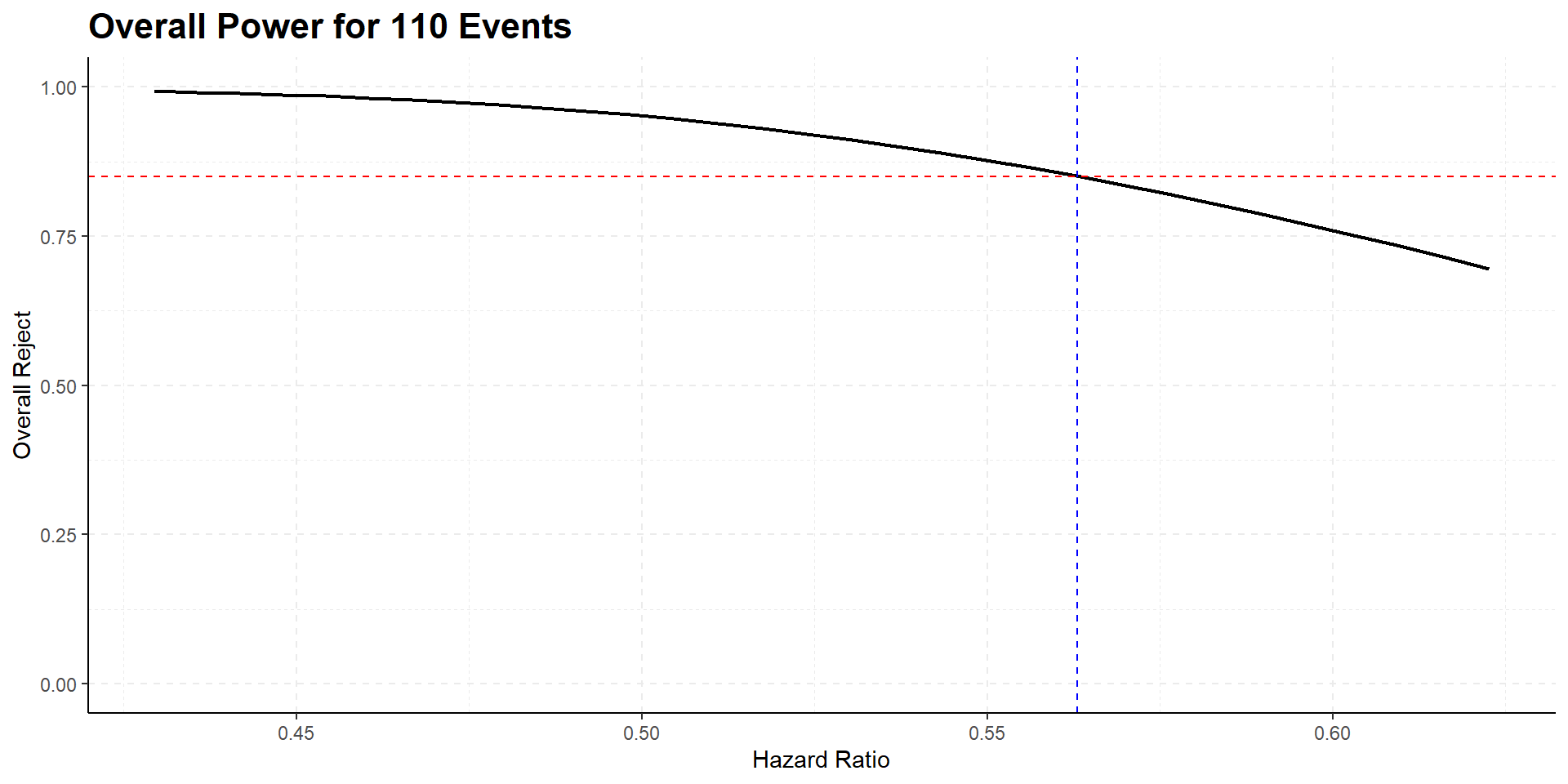
110 events are needed to achieve 85% power
262 study participants are needed to expect required number of events at given accrual and follow-up
drop-outs taken into account

325 planned participants are expected to achieve study goal in a shorter time frame

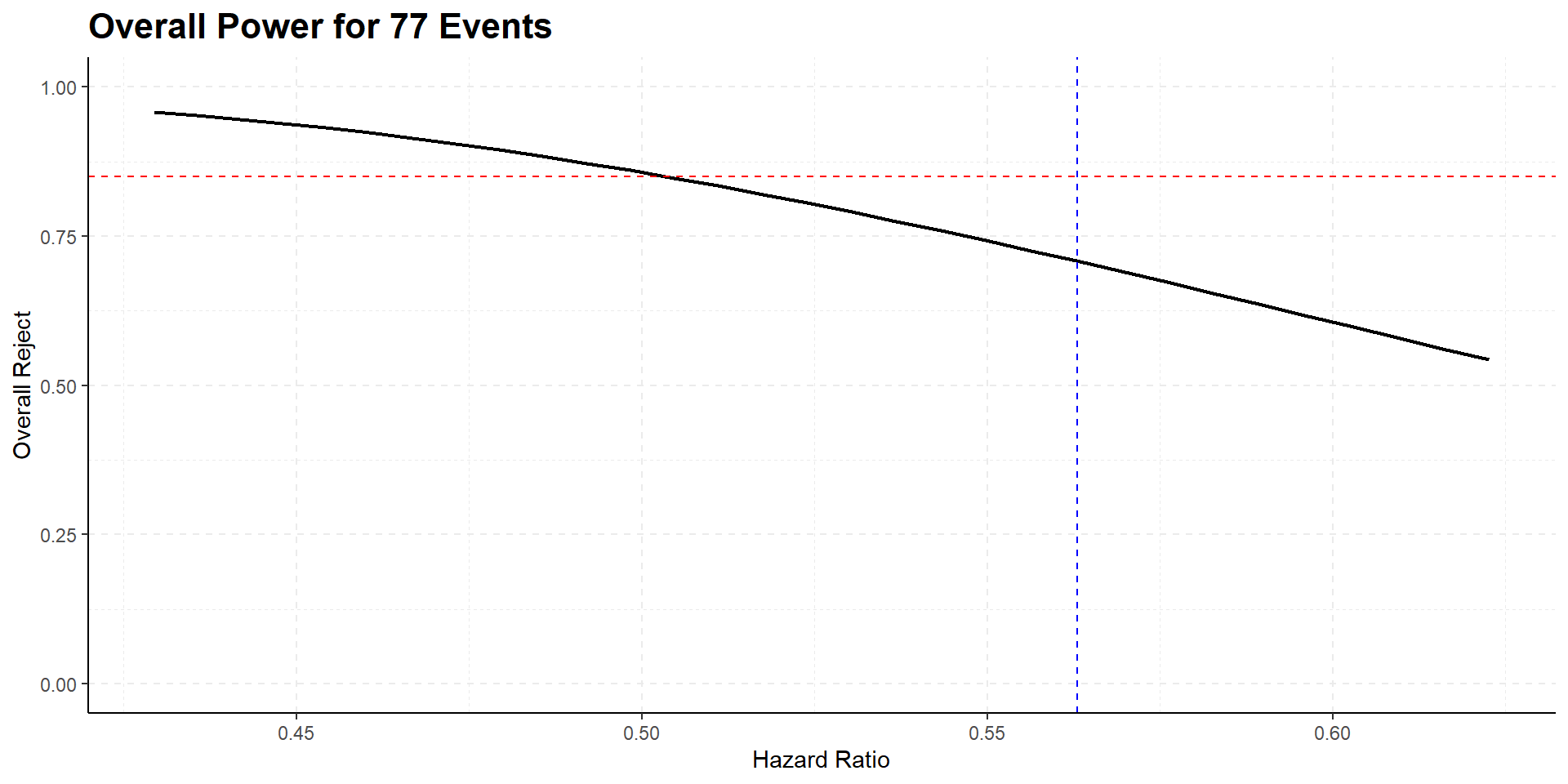
77 events do not achieve power 85%

Overall Power for 77 events

getPowerSurvival(
    design = designGS,
    pi1 = c(0.18, 0.25),
    pi2 = 0.37,
    eventTime = 6,
    maxNumberOfEvents = 77,
    maxNumberOfSubjects = 262,
    accrualTime = 24,
    dropoutRate1 = 0.25,
    dropoutRate2 = 0.25,
    dropoutTime = 6
) |>  plot(type = 7)

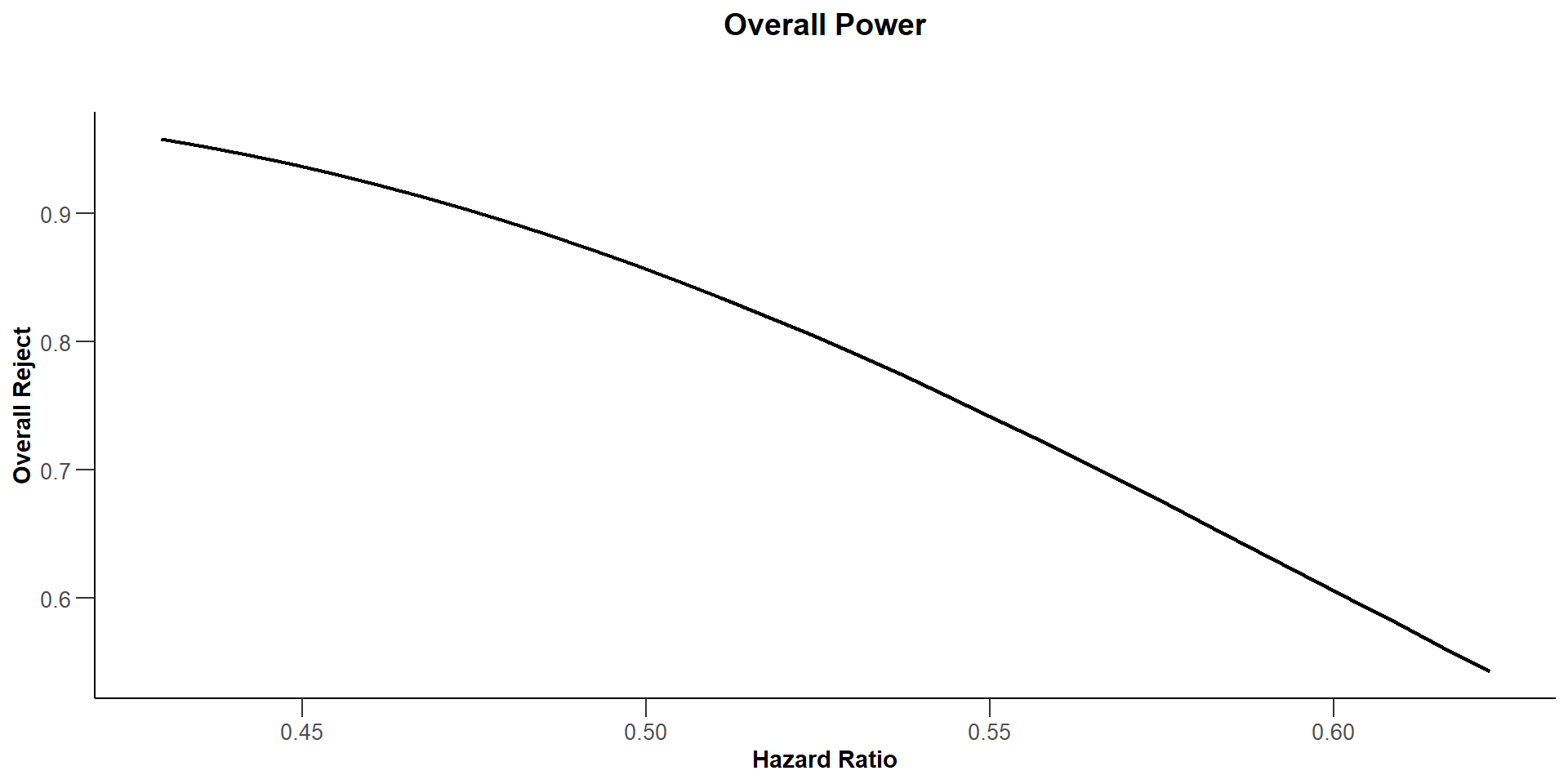
library(ggplot2)
library(ggpubr) # This for the grids
getPowerSurvival(
    design = designGS,
    pi1 = c(0.18, 0.25),
    pi2 = 0.37,
    eventTime = 6,
    maxNumberOfEvents = 77,
    maxNumberOfSubjects = 262,
    accrualTime = 24,
    dropoutRate1 = 0.25,
    dropoutRate2 = 0.25,
    dropoutTime = 6
) |>  plot(type = 7) + 
    ylim(0, 1) +
    ggtitle("Overall Power for 77 Events") + 
    geom_vline(xintercept = 0.563, linetype = 2, lwd = 0.5, color = "blue") +
    geom_hline(yintercept = 0.85, linetype = 2, lwd = 0.5, color = "red") + 
    theme_classic() + grids(linetype = "dashed") + 
    theme(plot.title=element_text(face = 'bold', size = 16)
)

When should the interim take place?

infRates <- seq(0.1, 0.9, 0.05)
power <- Vectorize(function(x) {
    getDesignGroupSequential(
        directionUpper = FALSE,  
        alpha = 0.025,
        typeOfDesign = "asHSD",
        gammaA = -4.5,
        informationRates = c(x, 1)
    ) |>
    getPowerSurvival(
        hazardRatio = 0.563,
        pi2 = 0.37,
        eventTime = 6,
        maxNumberOfEvents = 110,
        maxNumberOfSubjects = 262,
        accrualTime = 24
    ) |> fetch(overallReject)
})
ggplot(data.frame(infRates = infRates, power = power(infRates)), 
       aes(infRates, power)
      ) + 
  geom_line() + ylim(0.83, 0.87) + 
  geom_hline(yintercept = 0.85, linetype = 2, lwd = 0.5, color = "red") +
  ggtitle("Overall Power") +
  theme_classic() + grids(linetype = "dashed") + 
  theme(plot.title=element_text(face='bold', size=16))

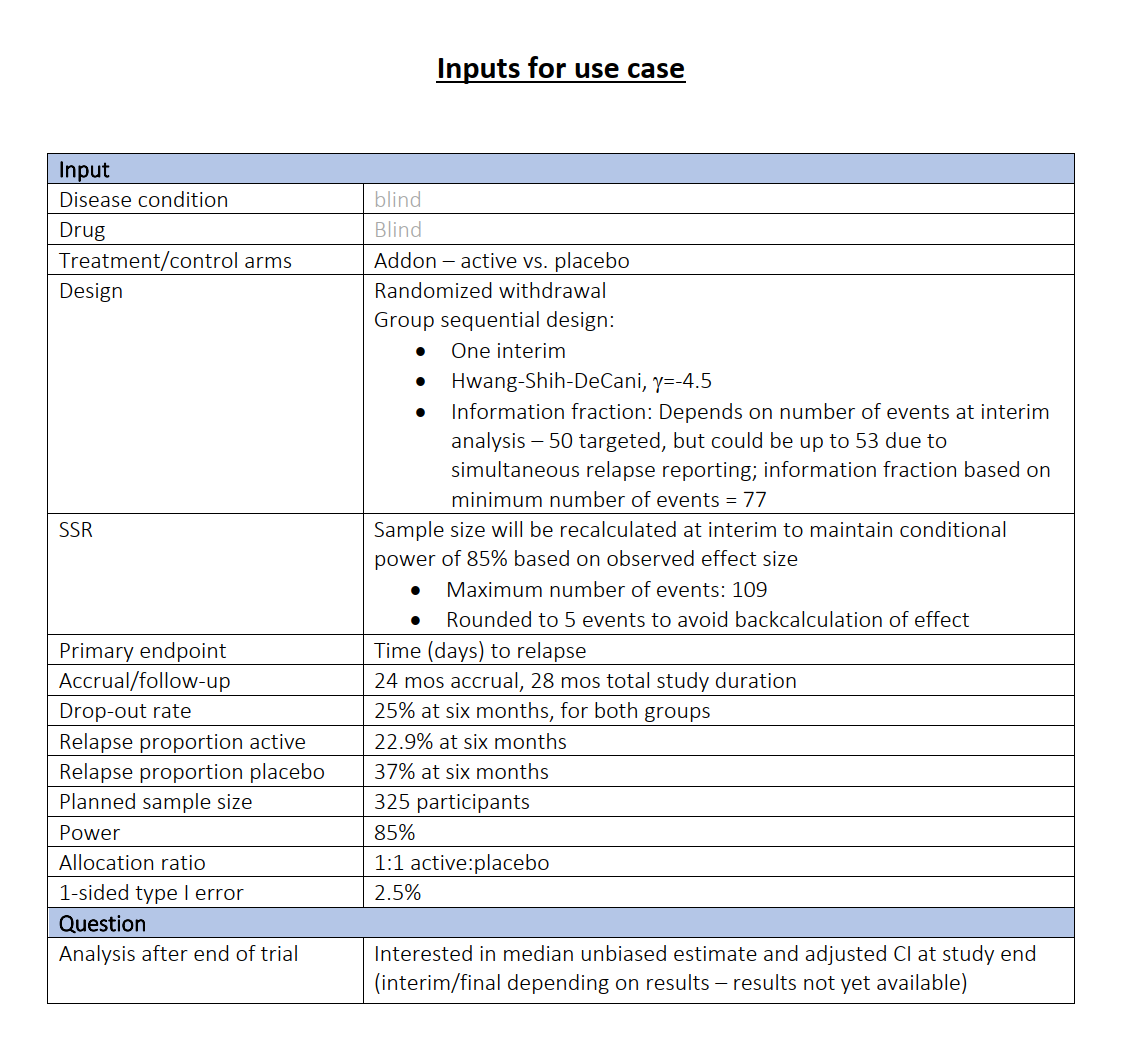
Varying interim time has no relevant influence on power

When should the interim take place?

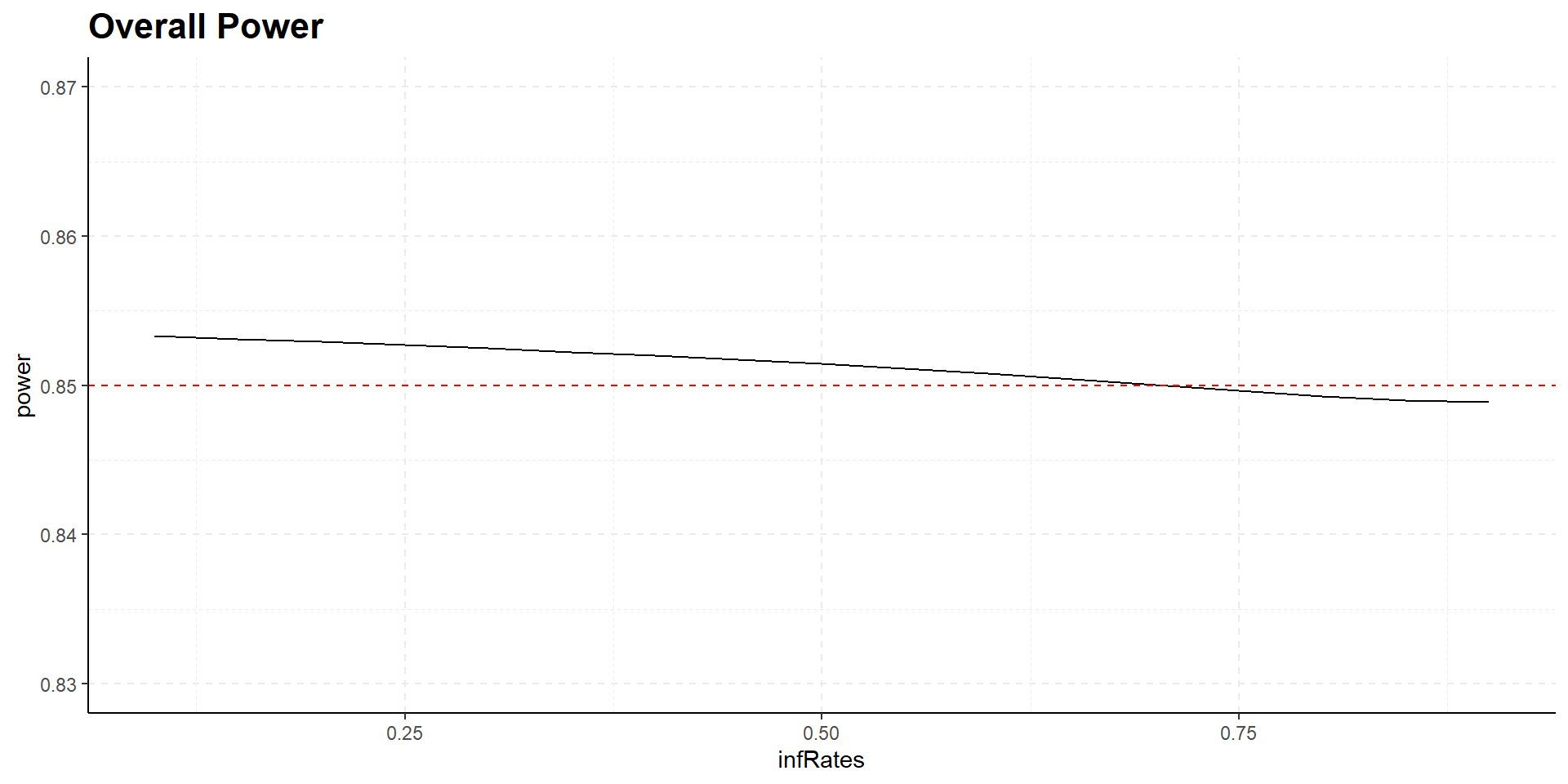
Interim time point has negligible influence on power but has effect on expected study duration, i.e., on expected number of events:

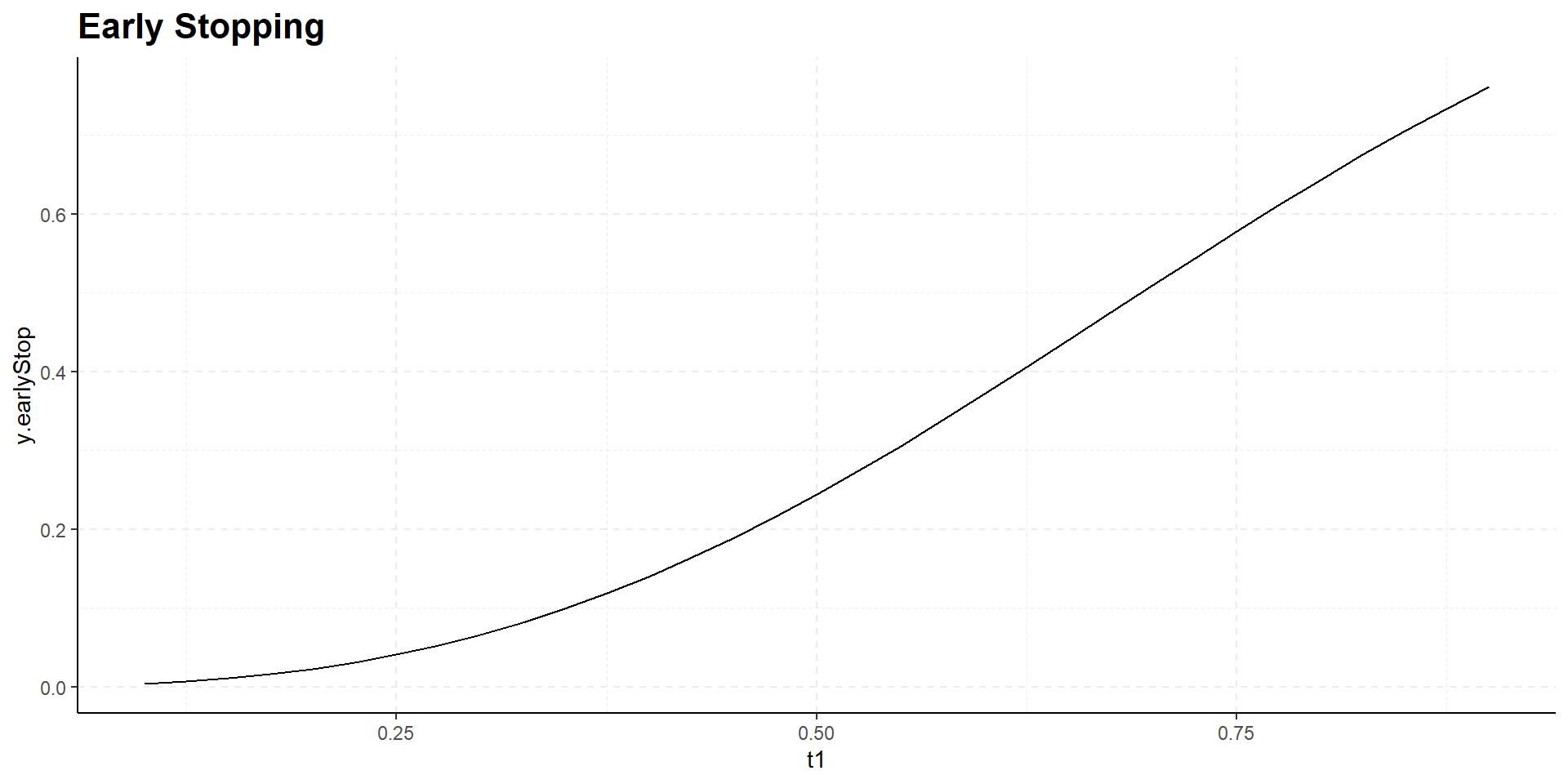
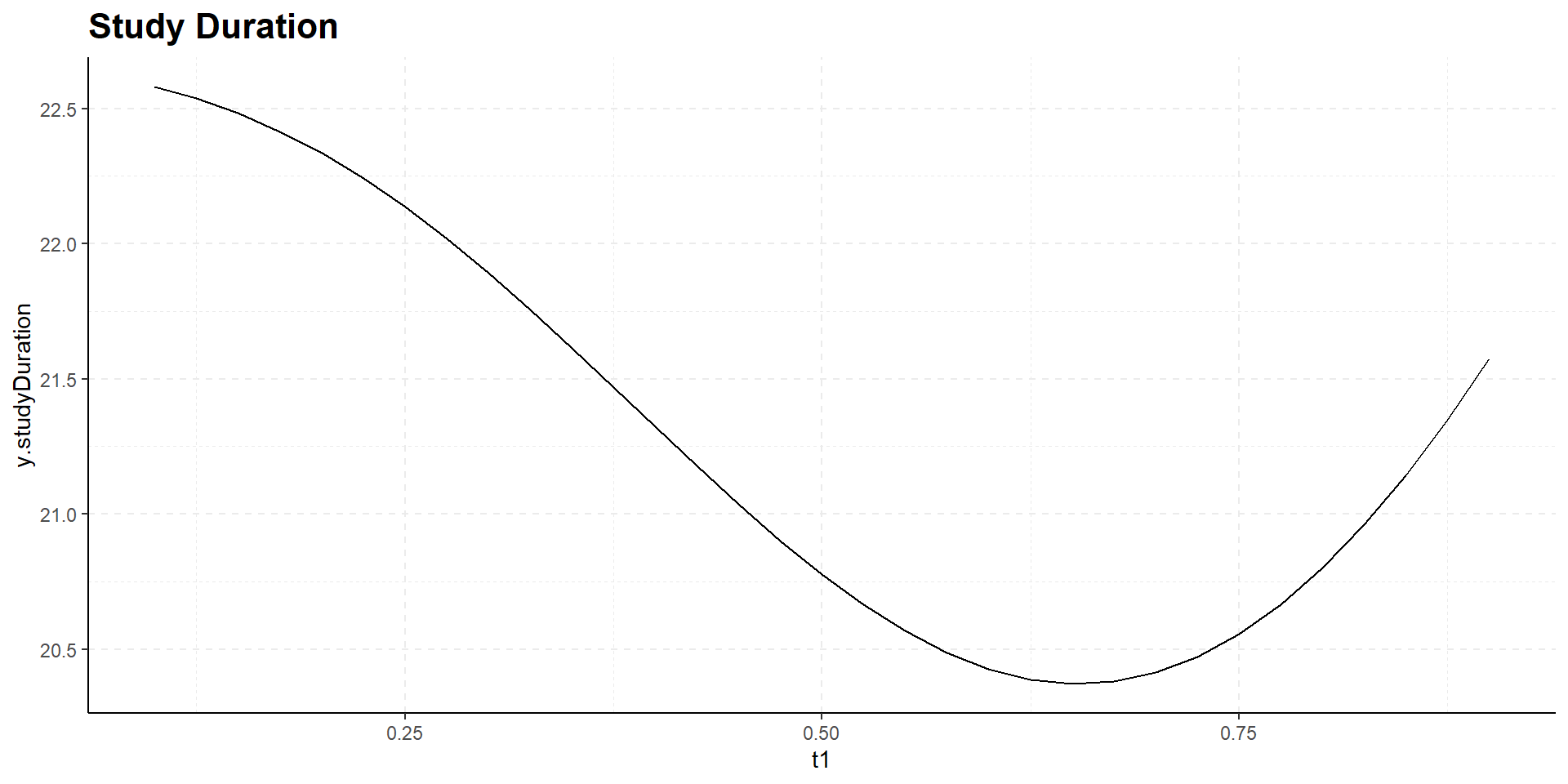
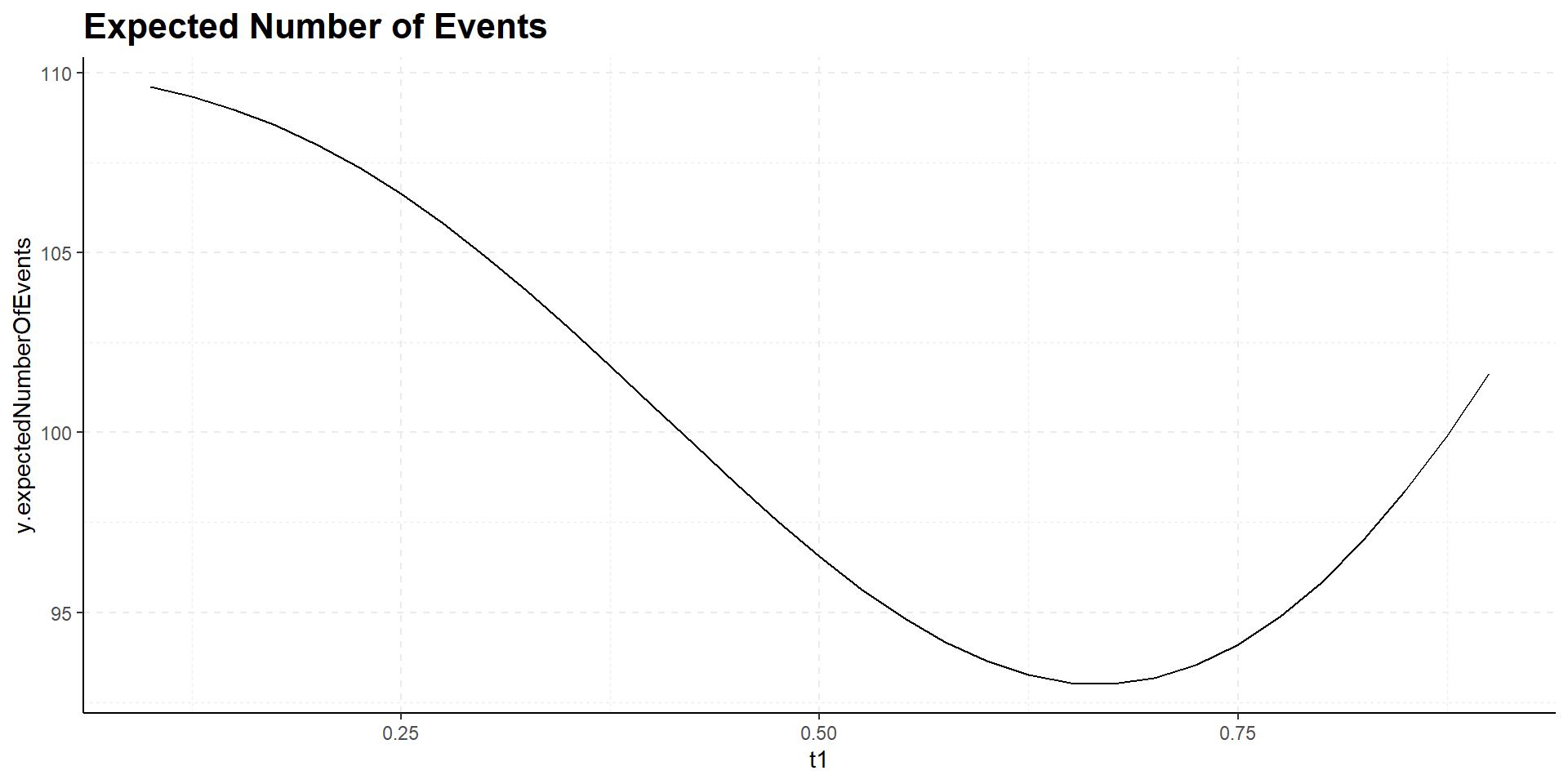
Design Considerations

Perform interim after observation of 77 events, then consider event number recalculation (“SSR”)
Use combination testing principle with pre-fixed weight for flexible recalculation.
Constrained promizing zone approach as a useful strategy.
For use in rpact, see Vignette Promizing Zone Design with rpact.
Analysis of trial according to Vignette Analysis of a Group Sequential Trial with a Survival Endpoint using rpact.
Conditional power calculation, calculation of repeated and final confidence intervals and p-values provided therein.

Case Study Survival Design

Case Study Survival Design

Survival Design

rpact Planning

Study specifications

Study specifications

Follow-up time can be reduced with 325 participants:

Design with interim stage

Design with interim stage

Results

When should the interim take place?

When should the interim take place?

Design Considerations

Questions?

`rpact` Planning